vertices of odd degree|Odd Vertex

vertices of odd degree,The ABS (atom-bond sum-connectivity) index of a graph G is denoted by ABS(G) and is defined as ∑xy∈E(G)(dx+dy)−1(dx+dy−2), where dx represents the degree of the vertex x in G. Abstract: We show that every cubic graph on $n$ vertices contains a spanning subgraph in which the number of vertices of each degree deviates from $\frac{n}{4}$ by .

Here is a proof by induction on the number of vertices. Consider first the base case when there is no vertex. Then the number of vertices of odd degree (or of any degree) is .

If a graph is connected and has exactly two vertices of odd degree, then it has at least one Euler path (usually more). Any such path must start at one of the odd-degree vertices and end at the other one.

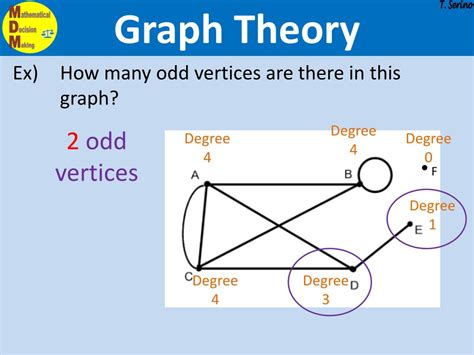
Odd Vertex. A graph vertex in a graph is said to be an odd node if its vertex degree is odd .

In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for .

The algorithm produces Eulerian circuits, but it can be modified to produce Eulerian paths if there are two vertices of odd degree. Suppose every vertex has even degree. Start with a vertex \( v \) and follow a path . An undirected graph has an Eulerian path if and only if it is connected and has either zero or two vertices with an odd degree. If no vertex has an odd degree, then the graph is Eulerian. Proof. It can be .A graph has an Euler path if and only if there are at most two vertices with odd degree. Since the bridges of Königsberg graph has all four vertices with odd degree, there is no .Theorem: Every graph has an even number of vertices with odd degree. Proof: The previous theorem implies that the sum of the degrees is even. The sum of the even .

Here exactly two vertices exist , but the degree of the vertices are odd. In this situation the odd degree are 1 or 3 in two vertices.In the undirected graph degree one have exactly connection between two vertex. In the case of 3 vertices both vertex have a loop (the loop consider as degree two in undirected graph) and a connected path between .

If zero or two vertices have odd degree and all other vertices have even degree. Note that only one vertex with odd degree is not possible in an undirected graph (sum of all degrees is always even . Before adding the edge, one of the vertices you are going to connect was of even degree, the other one of odd degree. Connecting them makes the even degree vertex into an odd degree vertex, and the odd degree vertex into an even degree vertex. So the number of odd degree vertices hasn't changed at all; in particular not from an .

In every graph, the number of vertices of odd degree is even. Proof Idea. Otherwise, the sum of the degrees of all vertices would be odd, which contradicts the theorem above. Example \(\PageIndex{3}\) An odd fellow throws an odd party and invites an even number of other equally-odd people. Each odd person at the party is friends . For a graph with two odd-degree vertices we take a first step of identifying a path between those two vertices. Removing those edges leaves the graph with only even-degree vertices, since the end nodes of the path ae reduced in degree by $1$ and all other nodes on the path by $2$. It is possible that the graph is now not connected, but this is .vertices of odd degree 5. Bipartite Graphs: A simple graph [Tex]G [/Tex] is said to be bipartite if its vertex set [Tex]V [/Tex] can be divided into two disjoint sets such that every edge in [Tex]G [/Tex] has its initial vertex in the first set and the terminal vertex in the second set. Total number of edges are (n*m) with (n+m) vertices in bipartite graph. Theorem: A simple . If no vertex has an odd degree, then the graph is Eulerian. Proof. It can be proven by induction that the number of vertices in an undirected graph that have an odd degree must be even. We will leave the proof of this fact to the reader as an exercise. The necessity of having either zero or two vertices of odd degree is clear from the proof of .

Two odd degree vertices belong to disjoint components. In this case, there are, by definition, two odd-degree vertices for which there is no path connecting them. And this situation can occur: just take the disjoint union of any .

what is our vertex? We thus require a total of 6 vertices of odd degree. We "require" a total of $6$ vertices of odd degree? Since we are given a graph with more than six vertices of odd degree it is not possible to construct a decomposition into three separate paths. this last part looks good, although it's simply repeating the thing we wish . All vertices have an odd degree (1 or 3), but the paths between all pairs are not disjoint.. graph-theory; Share. Cite. Follow asked Feb 28, 2012 at 1:37. pepsi pepsi. 489 4 4 silver badges 14 14 bronze badges $\endgroup$ Add a comment | 1 Answer Sorted by: Reset to default . Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this sitecircuits can start at any vertex. Euler’s Path Theorem. (a) If a graph has other than two vertices of odd degree, then it cannot have an Euler path. (b) If a graph is connected and has exactly two vertices of odd degree, then it has at least one Euler path. Every Euler path has to start at one of the vertices of odd degree and end at the .

vertices of odd degree Odd Vertex A path leads into a vertex by one edge and out by a second edge. So the edges should come in pairs (an even number). Only the start and end point can have an odd degree. Now Back to the Königsberg Bridge Question: .Odd Vertex Explanation: In any simple undirected graph, total degree of all vertices is even (since each edge contributes 2 degrees). So number of vertices having odd degrees must be even, otherwise, their sum would have been odd, making total degree also odd. Now single vertex n is connected to all these even number of vertices (which have odd degrees). I need some help understanding this proof. Full question: For some $k$, let $G$ be a connected graph with $2k$ odd-degree vertices, and any number of even-degree . Why can't we contruct a graph with an odd number of vertices

$\begingroup$ Ok, so for the base case say you have 2 3 cycles, these would both have even vertices. Then you connected 1 vertex from each together to give a total of 2 odd vertices. This would be an example of the base case with k = 1.

vertices of odd degree|Odd Vertex

vertices of odd degree|Odd Vertex .

Share:

×

Share

Copy Link

Email

Facebook

Twitter

LinkedIn

WhatsApp

Download: Full Size (80225 MB)

Photo By: vertices of odd degree|Odd Vertex

VIRIN: 44523-50786-27744